报告名称：Results and problems on graph edge coloring---I

报告专家：Guantao Chen

专家所在单位：佐治亚州立大学

报告时间：2024年6月12日14:00-18:00

报告地点: 数统学院201会议室

专家简介：陈冠涛，佐治亚州立大学教授，数学与统计系主任。主要研究方向为图论及其应用。主要研究图的结构问题，如图的圈和路、图染色和图的Ramsey理论。近年来，他的主要工作是研究对图的边进行重新着色的技巧，并利用它们解决该领域的一些经典问题。他在组合学和图论的主要期刊上发表了120多篇论文，并与他的许多合作者解决了许多长期存在的猜想。曾担任SIAM离散数学活动组的组织者(2014-2016)，以及《图与组合学》杂志的执行主编(2011年以来)。

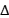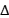报告摘要：An edge k-coloring of G is a mapping φ from E(G) to the set of integers [1,k] := {1, · · · , k}, called colors, such that no adjacent edges receive the same color under φ. The chromatic index of G, denoted χ′(G), is defined to be the smallest integer k so that G has an edge k-coloring. We say G is edge--critical or simply -critical if G is edge-chromatic critical and χ′(G) = + 1. Vizing conjectured that -critical graphs have some special structural properties. In this talk, we will present some recent progresses and still open problem on this topic.